Fibonacci-Zahlen

Was ist das?

Leonardo da Pisa, auch Fibonacci genannt (1170-1240), entdeckte die Fibonacci-Folge:

Man startet mit einer 1, dann folgt noch eine 1 und jede weitere Zahl berechnet man als Summe der beiden Vorgänger:

1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377 …

Johannes Kepler (1571-1630) entdeckte, dass sich das Verhältnis zweier benachbarter Fibonacci-Zahlen immer mehr dem Verhältnis des Goldenen Schnitts annähert.

Fibonacci-Zahlen in der Natur

Bei vielen Pflanzen ist die Anzahl der Blütenblätter eine Fibonacci-Zahl:
Orchidee (1); Euphorbia (2); Waldlilien (3); Akelei (5); Rittersporn (8); Ringelblumen (13); einige Astern (21); Gänseblümchen gibt es mit 34, 55 oder 89 Blütenblättern.

Bei Pinienzapfen gibt es 8 linksdrehende Spiralen und 13 rechtsdrehenden Spiralen:

Auch die Anzahl der links- und rechtsdrehenden Spiralen bei Sonnenblumen sind zwei benachbarte Fibonacci-Zahlen – selten sind Arten mit 21 und 34 Spiralen, meist sind es 34 und 55 Spiralen, Riesensonnenblume haben 144 und 233 Spiralen.
Ähnliche Phänomene sind zu beobachten bei: Ananas, Blumenkohl, Brokkoli, Disteln, Kiefernzapfen, Gänseblümchen, Margeriten, Dahlien und Kakteen.

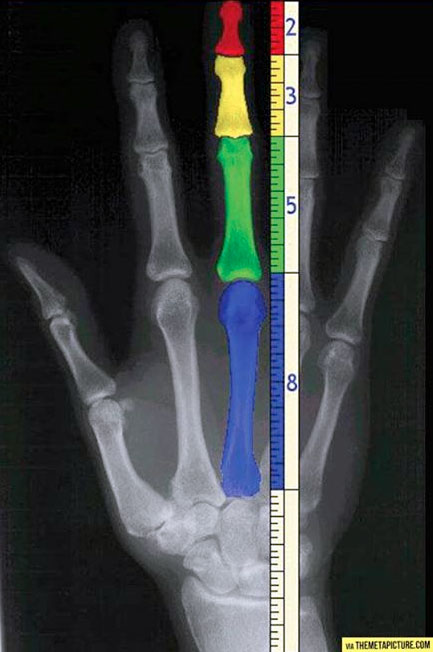
Auch an der Länge der Fingerknochen lassen sich die Fibonacci-Zahlen ablesen:

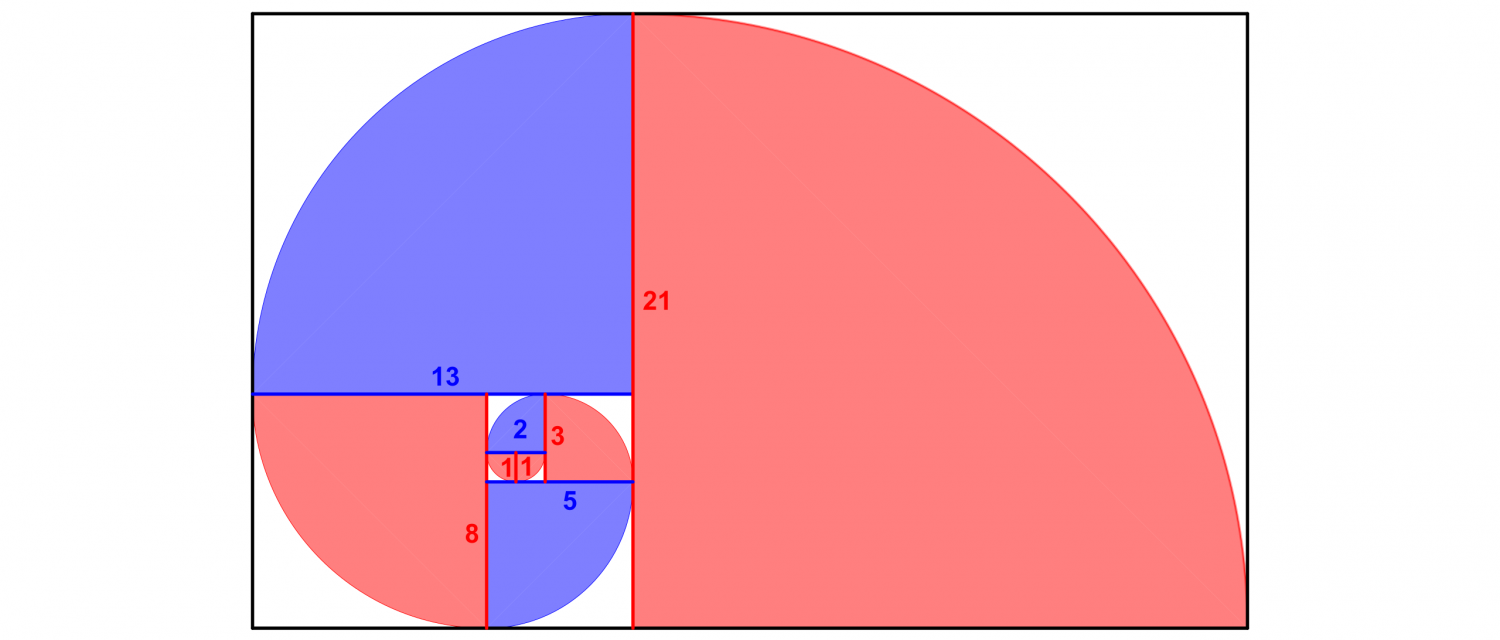
Die Goldene Spirale

Geht man von einem Rechteck aus, dessen Seitenlängen im Verhältnis des Goldenen Schnitts stehen und trägt man die kürzere Seite auf der längeren ab, entsteht ein Quadrat und ein neues, kleineres Rechteck, dessen Seitenlängen im Verhältnis des Goldenen Schnitts stehen. Führt man dies fort und zeichnet in den Quadraten jeweils einen Viertelkreis entsteht die Goldene Spirale. Die Seitenlängen der Quadrate ergeben hierbei die Fibonacci-Folge:

In der Natur kommt die Goldene Spirale häufig vor:

In Kunst und Architektur spielt die Goldene Spirale ebenfalls eine wichtige Rolle. Auf den Bildern sind das British National Wildflower Center, die Thanksgiving Square Chapel (Texas) und das Vatikanische Museum zu sehen.

Der Goldene Winkel

Um möglichst viel Sonnenlicht zu bekommen und um möglichst viel Regen abzufangen, um ihn zu den Wurzeln zu leiten bevorzugen einige Pflanzen eine bestimmte Position zwischen ihren Blättern: Das nächste Blatt, bzw. Seitentrieb wird um den Goldenen Winkel versetzt.

Den Goldenen Winkel erhält man, wenn man die 360° des Vollkreises im Verhältnis des Goldenen Schnittes teilt.

Fibonacci-Zahlen in der Welt der Mathematik

• Besonders häufig (unendlich oft) kommt der Goldene Schnitt in einem Pentagramm (Diagonalen eines regelmäßigen Fünfecks) vor.
• Mithilfe des Pascal’schen Dreieck kann man die Fibonacci-Zahlen berechnen.
• Fibonacci-Zahlen führen zu interessanten Teilbarkeitsproblemen.
• Einige kombinatorische Probleme führen auf die Fibonacci-Zahlen.
• Den Goldenen Schnitt kann man für die Konstruktion eines Ikosaeders verwenden.
• Für die Fibonacci-Zahlen gibt es eine Kettenbruchentwickung.
• Die Potenzen der Zahl des Goldenen Schnitts haben interessante Gesetzmäßigkeiten.
• Man kann die Fibonacci-Folge auch ins Negative fortsetzen.
• Für die Zahl des Goldenen Schnitts gibt es eine Wurzelentwickung.
• Informatiker benutzen sog. Fibonacci-Bäume für Effizienzüberlegungen
• …